Structures - Nodal Analysis Practice

Here is the question we did today:

First I took the bottom node to work out the internal forces in B and A.

I then took the middle node.  To build on last time's question this node now has a force acting on it and so C is not redundant.  Simultaneous equations are now required to solve the forces here.

Because we now know the force in D, we know that the reaction X in the wall is equal and opposite to it.

And finally looking at the bottom node we can work out the reaction Y.

Structures - Nodal Analysis Practice

Here is the practice question we did today:

 

First of all we can find the reaction of the roller using moments:

 

Then I took the top node first to do nodal analysis:

Then I moved down.  C is clearly redundant as e and a act in a straight line and if you remove c you still have a triangle. (If there was an external load at this node then that would effect the internal forces in C and it would no longer be redundant.)

I moved down again to work out the force in d.

I could then look at the last node to find the reaction of the hinge.

Structures - Practice after Homework

Today we did a couple more questions together.

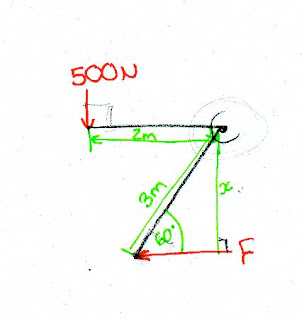
First of all we looked just at moments with forces which are not acting perpendicularly onto the beam.  This means that we must resolve these forces into their component parts to find the magnitude of the component which acts perpendicularly to the beam.  To help do this, I would have turned this question so that the beam was horizontal, this is how my working is done.

Then we looked at finding a hinge reaction. First of all we needed to use moments to find an unknown force. 

Two methods are shown below:

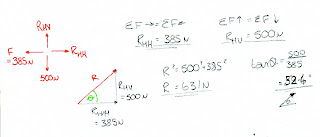
A moment is the force x the perpendicular distance.  The 500N force is already acting at right angles to the beam so the anticlockwise moment is simple to calculate.  The unknown force is not acting at right angles to the beam it is acting on. So we need to find the perpendicular distance of this force to the hinge.

The alternative is to resolve F into its components and work out how much of F is acting at right angles to the beam.  This can then be multiplied by 3 to find the clockwise moment and therefore the magnitude of F.

Now that you know all the forces acting on this beam you can work out the hinge reaction.  The very first thing to do is draw an up/down right/left diagram to calculate the components of the reaction, and therefore use pythagoras to work out the hinge, and trig to work out the angle.

Case Study

For the last class period of Case Study we looked at the introduction and conclusion.

Therefore your completed Case Study should be handed in on:

Monday 12th December

Introduction:
You need to briefly introduce your topic.  State what you will study and how you will go about it.  Are you focusing on a specific aspect of technology?
This should be around 250-300 words.

Conclusion:
This must be written in your own words as it is your summary of what you have found.  Sum up your findings and make a final statement about what you found based on your research and analysis.
This should be around 300-400 words.

Bibliography/References:
You must include where every piece of text, diagram or picture was sourced.  This could be done by putting little reference numbers throughout your report and then listed at the back with where these came from, or just a list of references.

Books: Author surname and initials, (Year), Title, Publisher, Place of Publication, Page Numbers

Journals: Author surname and initials, (Year), Title of article, Name of Journal, Volume number (and part), Page numbers

Websites

Structures - Outcome 2 - Nodal Analysis

We need to be able to find the forces in different frame structures.

The first thing we need to look at are how the members react under different applied forces.  We need to therefore look at the internal forces in members:

Knowing this, we can look at analysing structures.  We will need to use our previous knowledge of how to resolve forces into their component parts, and the conditions of equilibrium: vertical forces, horizontal forces and moments.

Stages for Nodal Analysis:

•  Work out any unknown external forces using moments (where possible)
• Mark on your freebody diagram the directions of all the internal forces
• Take the nodes in turn - start with the node you know the most information for.
• Redraw the node.  Redraw and resolve any forces at an angle.
• Draw an up/down, right/left diagram
• Find out your unknowns and state whether the member is a strut or a tie.
• Move on to the next node
• Remember that there may be a hinge reaction at a node, in which case you need to make sure that you work out the horizontal and vertical components of it, and then use Pythagoras to find the magnitude and trig to work out the angle.

Now here is the worked example on page 2.  Take some time to make sure you understand the different stages of the nodal analysis.

Structures - Outcome 1 - Forces and Moments

We need to be able to work out beam reactions with simple (pivots), roller (straight up) and hinge reactions.  We can use moments in the same way as we have been previously for simple supports and rollers, however hinges will have a reaction equal and opposite to all of the horizontal and vertical forces acting on the beam.

Here is an example:

Here is a more challenging example of using moments and forces at an angle. We did this today on the board.

Homework 7 on moments and forces is due on 21/1/11

Structures - Outcome 1 - Forces and Moments Introduction

First of all we needed to revise some concepts from Intermediate 2:

Mass: Is the bulk of an object - the amount of "stuff" which makes up a body.
Weight: Is the force that body has due to the Earth's Gravitational Field strength (9.81m/s/s) because F = m.a
Moment: The turning effect of a force.  It is found using: M=Fd (force x distance)

We then reminded ourselves of the conditions of equilibrium:

And from that did some work on moments:

Using R1 as our pivot we could use moments to find R2:

Then use the vertical forces to find R1:

In Higher, however, we will also have to deal with forces which act at an angle.  To be able to work with these forces we must be able to convert a force into its horizontal and vertical components:

Case Study for Today

Today we are looking at the impact of your project on the wider world under the headingsSocial, Economic and Environmental Effects.  This section should be around 350-450 words.

These questions could be useful to you:

Social Effects:

• Have jobs been created or lost, directly or indirectly through use of this technology?
• Have lifestyles been changed through this technology?
• Have cultures been changed through this technology?
• Have these effects been positive or negative? Explain

Economic Effects:

• Has this technology increased profits/income for people or companies?
• Has it affected economies?
• Does it provide cheaper/more expensive products/technology?
• Is it expensive to own and use/run this technology?
• Have any of these effects been positive or negative? Explain.

Environmental Effects:

• Has this technology had an environmental effect for people. cultures or companies?
• Is the product recyclable/made from recycled components?
• Has it effected the natural/urban environment, directly or indirectly?
• Does the product manufacture use/provide environmentally cleaner/dirtier products?
• Have these effects been positive or negative? Explain.

You also had to submit a first draft of your analysis and description.

Applied Electronics - Outcome 1 & 2 Practice Questions

Here are some questions for you to try over the October break. I may put some more up later, but here are some to get you started.  Remember that a lot of the NAB is description, so put extra effort into the describe questions!

 

For the question above, please note that ID should be 10mA, not 20mA, the supply voltage should be 24v, and that the thermistor is a type 4 thermistor.  Sorry for the edit! 

Applied Electronics - Outcome 3 - Boolean Algebra

Boolean Algebra is another way of describing a logic truth table or circuit.  Just like any other Algebra you need to know the operators to be able to write the equations.

They are:

You need to be able to go between an English statement, a truth table, a logic circuit and a Boolean expression.

From a Boolean expression you can work out which logic gates you will need to perform each part:

To derive a Boolean expression from a truth table you must identify when the output is on, writing an expression for these lines and then combining each of these expressions with an OR operator.

You can also derive a Boolean expression from a circuit diagram by following the signal using the original inputs and the Boolean operators:

Applied Electronics - Outcome 3 - Logic

Outcome 3 is logic.  It is not vastly different from Intermediate 2, but they may ask you to design a more complicate circuit and look at NAND or NOR equivalents.

Firstly lets consider this circuit:

The first thing we should be able to do is draw the truth table for it:

A and B are our two inputs, but we could put in points to help us after the AND gate (C) and after the NOT gate (D).

A B   C   D   Z
0 0     0    1   1
0 1     0    0   0
1 0     0    1   1
1 1     1    0   1

We could also draw the NAND and NOR equivalent circuits.  By taking one gate at a time we can draw the equivalent for that gate, and then connect them as the original circuit is.

The benefit of designing a NAND equivalent is that we then only need one type of chip.  This makes it cheaper as we have simplified the circuit to only need one type of IC, and we could get a smaller end product as we need to include less ICs.

Here is the NAND equivalent of the above circuit.  Notice that there are two inverters in a row so they cancel each other out.  Instead of drawing the whole circuit again, you can simply put a line through them.

This has really simplified the circuit!  Instead of needing 3 ICs we now only need one, and we only need to wire in two gates.

This is the NOR equivalent.

This is less effective for this circuit as it has actually given us more logic gates to wire.  But we do only need 1 IC instead of 3.

Applied Electronics NAB

Your NAB for Applied Electronics will be on:

Friday 28th October

You will need to be able to:

•  Carry out calculations and describe Transistor and MOSFET circuits
• Identify, describe and carry out calculations for the different configurations of Op-Amps

Applied Electronics - Outcome 2 - Operational Amplifiers

Operational Amplifiers are components which can be configured to have many uses.  You need to know about 6 of these configurations.

General Information about Op-Amps:

• They have an infinite gain (open loop)
• They have an infinite input impedance (resistance) and so no current flows into the Op-Amp
• They have no output impedance
• There is no difference in the potential between the two inputs

• The Op-Amp has two terminals: A non-inverting terminal (labelled +) and an inverting terminal (labelled -)
• It normally has a positive and a negative supply so all voltages are measured relative to ground.
• Like transistors and MOSFETs if the Op-Amp is fully switched on, it is saturated.

These pictures (from this website) show the pin out diagram of the 741 Op-Amp chip.

Op-Amps can be open loop or closed loop.  If open loop they have no feedback and therefore the gain is infinite.  The first open loop Op-Amp to consider is the comparator.

This compares the two inputs named here as Vi and Vref. Vi goes to the inverting terminal and Vref to the non-inverting terminal. 

• If Vi > Vref then the Op-Amp will saturate negatively so Vo = (85%) -Vcc
• If Vi < Vref then the Op-Amp will saturate positively so Vo = (85%) +Vcc

Due to the characteristics of the Op-Amp in reality, it will saturate at 85% of the supply.

The other open loop configuration you need to know about is the voltage follower.

The two simplest, closed loop Op-Amps are the non-inverting and inverting amplifiers.

Inverting:

The inverting amplifier has a feedback loop with a feed back resistor Rf.  The configuration of this and the input resistor, Ri gives the Op-Amp a gain.  This means that the input voltage is amplified to give the output voltage. 
The gain is found using the equation: Av = -(Rf/Ri)
The output voltage is found by multiplying the Vi by the gain: Vo = Av.Vi, so Vo = -(Rf/Ri) . Vi


Non-Inverting:

The non-inverting amplifier also has a feedback resistor to create a gain.
The gain is found using the equation Av = 1+Rf/Ri
The output voltage is therefore found using the equation Vo = 1+Rf/Ri . Vi

The most important thing to remember about the non-inverting amplifier is to remember about the 1!  This can sometimes make the non-inverting amplifier unsuitable as it always has a gain of more than 1 and you may need a decimal gain.  In this situation you may need to use two inverting amplifiers, one to give the gain and one with a gain of -1 to invert the signal back to a positive one.

Difference Amplifier:

The difference amplifier magnifies the difference between the the two inputs.

Summing Amplifier:

The summing amplifier is used to combine more than one input voltage to give an output voltage.  This is done by multiplying each input by a gain (Rf/Ri) and adding them together.  The inputs can be given different gains depending on their importance/input voltage.  i.e. if a input produces a small voltage, you can make the gain for that input bigger in relation to the others to give it equal importance.

In this way, a summing amplifier can be used as a digital to analogue converter.  Because a microprocessor can only give a high or a low signal, the output will always be either 5v or 0v.  So if you have a signal of 1001, decimal 9, the output voltage should reflect this.  By 'weighting' the input resistors you can create a DAC.

Tachogenerator investigation

This is my experiment to see if I can upload a video onto the blog from the iPad! Hopefully you can see the investigation we did today to see if the tachogenerator generated a linear output proportional to motor speed.

Case Study for Today

Today in our case study period you should have started looking at the Analysis and Description section of the case study.  This should be between 500 and 800 words.

Start by researching how your product works.  You should be able to draw (or find) a system diagram which helps describe the parts of your product and how they work together to produce your output.  Once you have a very general description, and a general system diagram, you should break your system down further to describe it in more detail.  A more detailed system diagram should then be described.

To help you check through this section you may find these questions useful:

• Are all my systems diagrams clear?
• Is there an overall, simple diagram with inputs, outputs and feedback?
• Are all the components clearly identified and analysed in a paragraph after the diagram?
• Has the system been fully analysed and explained?
• Has an evaluation of the technology involved been achieved?

Make sure that you keep a note of all the websites you have used to get information and/or pictures from.  You need to reference these properly at the end of your case study report.

Applied Electronics - Outcome 1 - MOSFETs

MOSFETs at a glance:

N-channel MOSFET

• MOSFETs are similar to transistors, but they are voltage operated devices. 
• This means that (ideally) it draws no current. (This means that you can use ohm's law in your calculations to find the Vin unlike a transistor where you must use the voltage divider equation because the transistor will draw current from the supply/voltage divider)
• They can be N-channel, or P-channel
• It has a very high input resistance, and no (low) current, therefore has a low power consumption
• It has a slower switching speed than a transistor
• It is very sensitive to static!  Beware when building with them!

•  MOSFETs operate above a threshold voltage VT.  When the voltage between the gate and the source (VGS) is above the threshold voltage, the MOSFET will saturate and ID will be its maximum and will not increase past this point.
• Until full saturation the ID will increase proportionally.  It is then possible to calculate the transconductance which is the ratio between ID and VGS as demonstrated below:

•  MOSFET circuit calculations involve mostly ohm's law.  This diagram shows the voltages dropped and the currents in the circuits:

 

So, a similar question to the homework - Use the diagram above to help you understand the labels and relationships between the voltages and currents.

This MOSFET has a Threshold voltage of 5v. When saturated the ID is 3mA and the source resistor is 2k (The supply voltage is 12v).  The current flowing through the voltage divider is 5uA.

Find the values of R1 and R2 (in the voltage divider) to ensure saturation.

So if ID = 3mA then IS will equal 3mA.  If the source resistance is known then the VS can be found.

VS = ISRS

        = 3x10-3 x 2x103 

        = 6v 

If we know VS and we know VGS (remember that if the MOSFET is saturated then VGS = VT) so we can find VG which is the voltage dropped over R2.

VG = VGS + VS

       = 3 + 6

       = 9v

If we know VG and we know that the current flowing through the voltage divider, then we can work out the two resistances.  Remember that we can use Ohm's law because no current goes into a MOSFET so it is all flowing through the voltage divider.

 VG = V2 = IR2

           9  = 5 x10-6 x R2  

         R2 = 9/5 x10-6

               = 1.8M Ω

V1 = VCC - V2              R1 = 3/5 x10-6

      = 12 - 9                 = 600kΩ

      = 3v 

Find the VDS if the Drain resistor is 500Ω.

 VD = ISRS                                      VDS = VCC - VD - VS

          = 3x10-3 x 500                 = 12 - 1.5 - 6

          = 1.5v                            = 4.5v